Shading

Introduction

The term shading describes the light fall-off or color variation from the sensor center to the corners that do not originate from the captured scene. In other words, shading is a decrease of the image brightness from the center to the corners. Occasionally a variation of color over the imaging field can occur, particularly in cameras with a small sensor. Overall, shading influences image quality by creating unwanted dark or shaded edges.

The background of shading

When visualizing the shading of a camera system, it is easiest to capture a flat field image, a photograph of white paper with uniform illumination, or a photograph of a uniform diffuse light source such as the opening of an integrating sphere.

The minimum shading an optical system has is that of the cosine law described in photometry. The optical design of the system can increase it. Vignetting can occur from the lens or other objects' physical limitations, such as improper lens filters or false lens hoods.

Types of shading

ISO 17957 breaks down shading into two main categories for measurement.¹ The first category is luminance shading, which the standard defines as a variation of the luminance signal components within the image field. The second category is color shading, a variation of the chrominance signal components within the image field¹.

Luminance shading

Luminance (also known as lightness) shading can be broken down into a few separate groups depending on where the shading occurs.

Natural shading (cos⁴ law)

Natural shading is when there is a light fall off from the center of the image to the corners. This type of shading is simply caused by geometry.

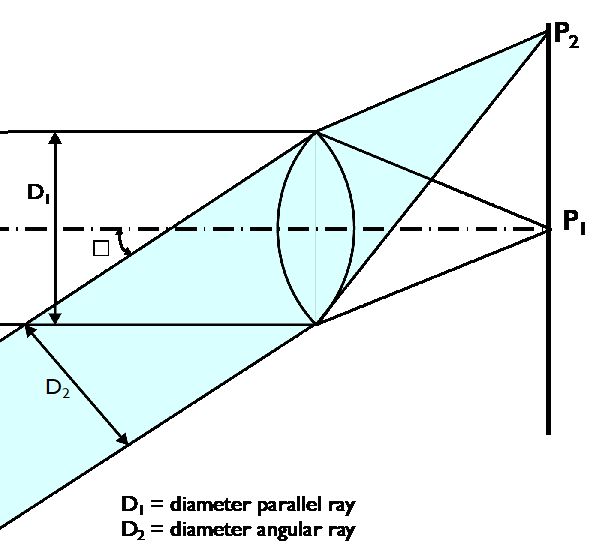
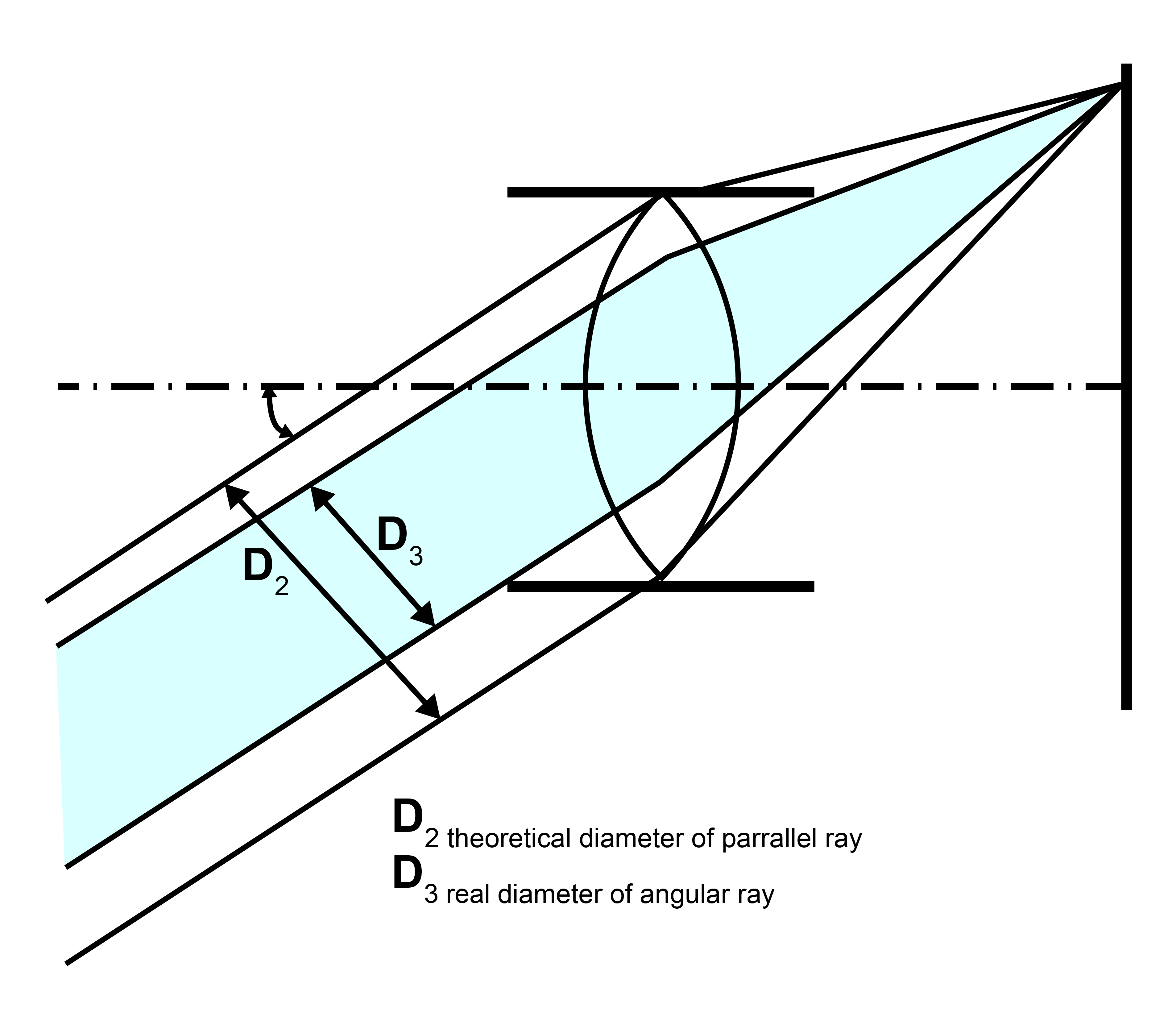
Figure 1 illustrates that the distance (D₂) is D₁ multiplied with the cosine of δ. It’s best to think of D₂ and D₁ in two dimensions (or rather areas instead of dimensions), and thus the energy moving from D₂ towards the lens is the energy of D₁ multiplied by (cos δ)². We now also have the same situation on the lens's incident side as the energy transmitted by the lens is D2 multiplied by (cos δ)².

Both of these areas together result in the cos⁴ law:

E(P₂) = E(P₁) * (cos δ)⁴

The maximum amount of natural shading in an image is determined by the camera's field of view. For example, a wide-angle image contains more natural shading than a telephoto image.

Mechanical shading or vignetting

Another part of luminance shading is known as mechanical shading or vignetting. The cause of this type of shading is the lens mount or other accessories such as the lens hood. It usually depends on the aperture or f-number, and smaller apertures usually show lower mechanical shading.

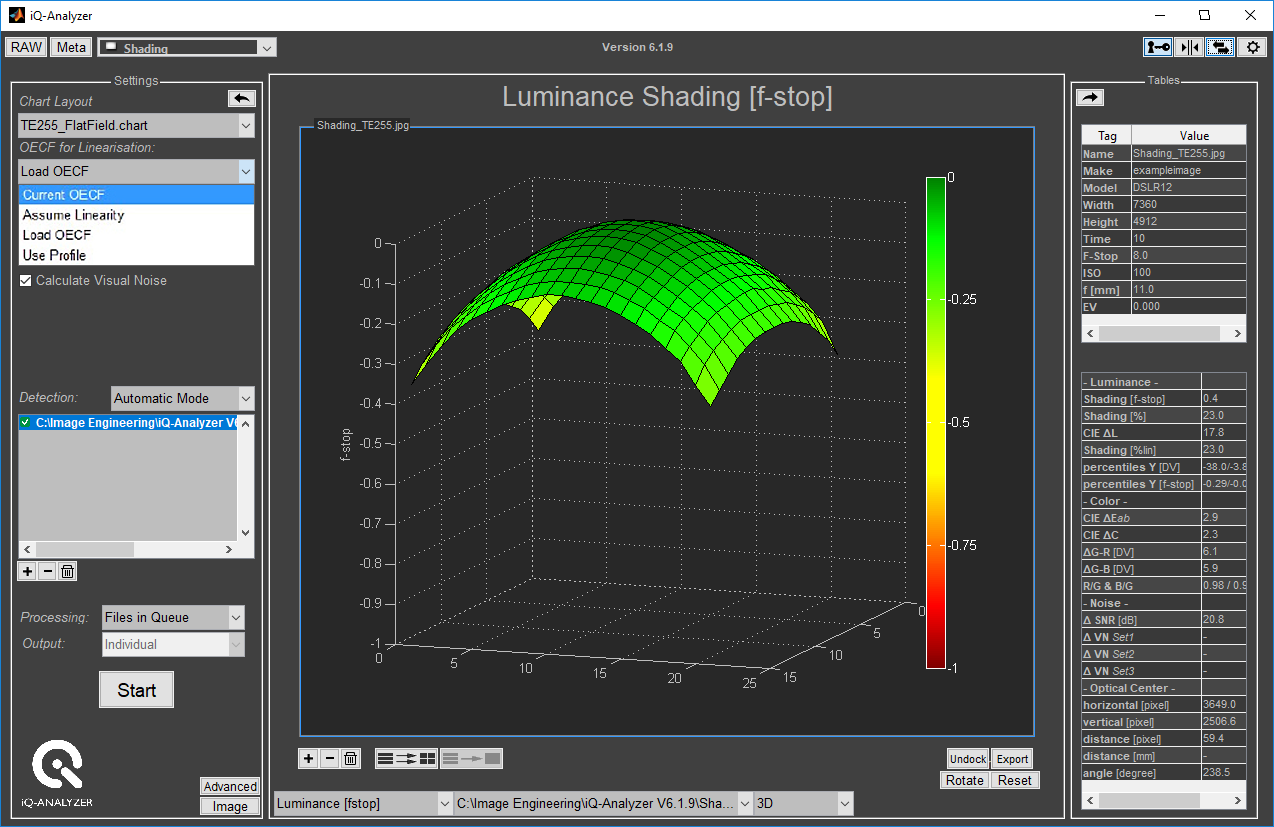
Measuring luminance shading

When measuring luminance shading, ISO 17957 differentiates between the CIELAB method of "lightness non-uniformity" and the X, Y, Z method of "luminance non-uniformity" using two related formulas. The standard describes the measurement in detail.

Lightness shading:

$$D_L=max\left[L^\ast(i)\right]-\left[L^\ast(i)\right]$$

Luminance shading

$$D_Y=\frac{max\left[Y(i)\right]-min\left[Y(i)\right]}{\max\left[Y(i)\right]}\ X\ 100$$

With the measurement results of luminance shading, a polynomial fit can be calculated and used to brighten the corners to compensate for the shading. Thus, compensating for a moderate shading level can be done in the camera imaging piper or during raw image processing.

Color shading

Color shading (or color non-uniformity) usually describes a shift in color from the center of the image to the corners. This type of shading typically occurs in images captured with a camera with a smaller sensor. Color shading has multiple causes, including the two most common types, pixel crosstalk off-axis, and the IR-cut filter transmission.

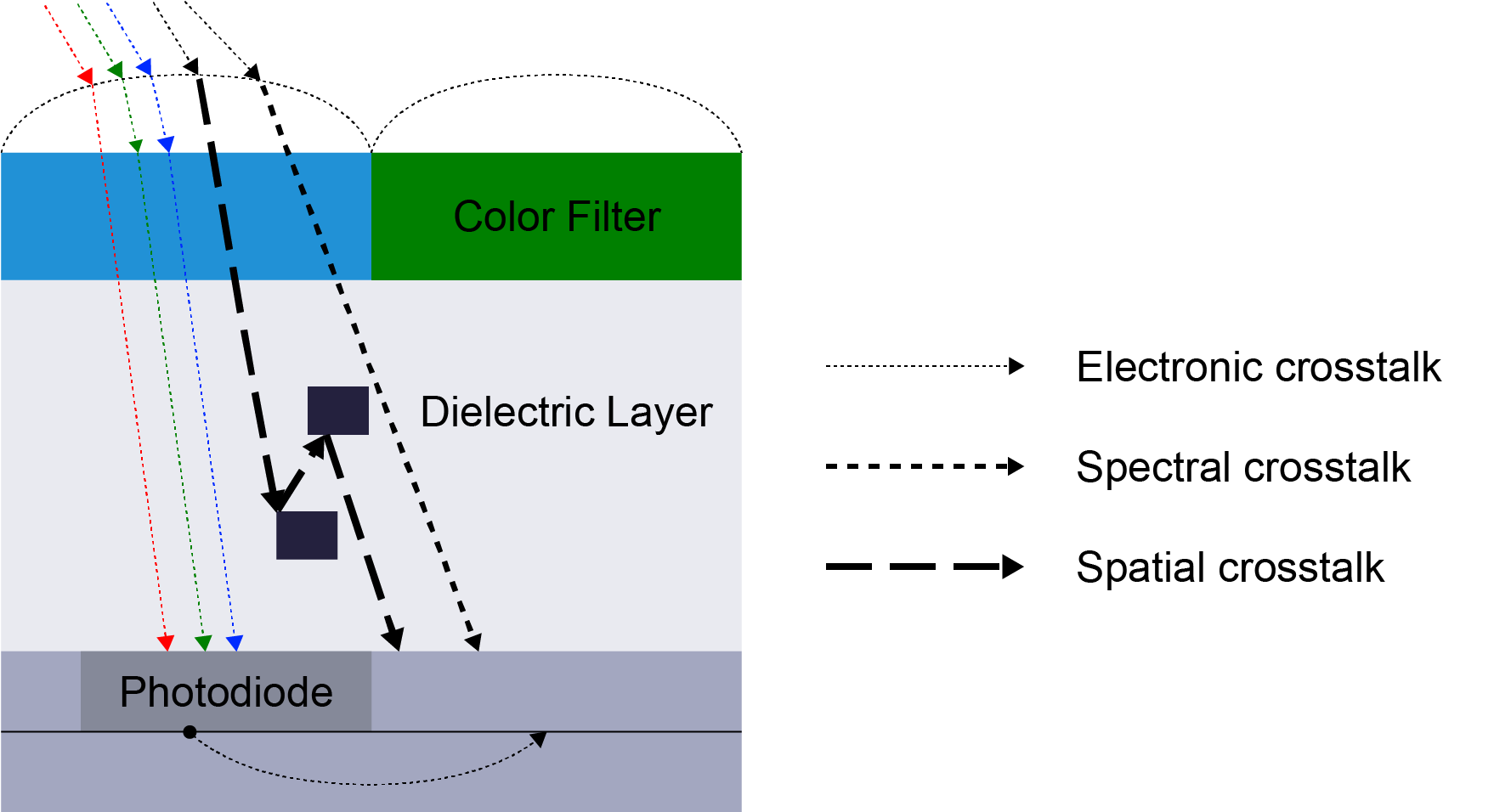
Pixel crosstalk color shading

Pixel crosstalk off-axis describes an increase in the spatial variation between (crosstalk) the pixels. Lenses that are not designed as near telecentric can often experience pixel crosstalk shading.

IR-cut filter

The transmission of the IR-cut filter shifts towards a shorter wavelength as the angle of incidence increases. The IR-cut filter shift has a more substantial impact on the image if the light source contains a lot of IR radiance like natural sunlight or incandescent lights. Fluorescent tubes or LEDs do not display this phenomenon as often due to the lag of the IR content in their spectrums.

Measuring color shading

ISO 17957 outlines two separate formulas for measuring color shading. The first formula describes the chrominance non-uniformity and focuses on the differences in the a* and b* channels. The second formula details the total color non-uniformity, which takes into account the lightness L*.

Chrominance non-uniformity

An analysis of the chrominance non-uniformity is performed by first calculating the overall average (a*) ̅ and (b*) ̅ for the entire image using the block average values: a^* (i) and b^* (i).

$$\overline{a*}={1/m}\cdot\sum_{i=1}^{m}{a\ast\left(i\right)}\space\space \overline{b*}={1/m}\cdot\sum_{i=1}^{m}{b\ast\left(i\right)}$$ $$m:\mathrm{number\ of\ measurement\ blocks}$$

Calculate the chrominance deviation of the i block with the following formula.

$$D_c\left(i\right)=\sqrt{\left[a^\ast\left(i\right)-\bar{a^\ast}\right]^2+\left[b^\ast\left(i\right)-\bar{b^\ast}\right]^2}$$

The chrominance non-uniformity Dc is defined as the maximum deviation from the overall average of the following formula.

$$D_c=\max{\left[D_c(i)\right]}$$

Total color non-uniformity

An analysis of total color non-uniformity begins by first calculating the overall maximums and minimums of L*(i), a*(i), and b*(i).

$$L_{max}^\ast=max\left[L^\ast\left(i\right)\right],\ \ \ \ \ \ L_{min}^\ast=min\left[L^\ast\left(i\right)\right]$$

$$a_{max}^\ast=max\left[a^\ast\left(i\right)\right],\ \ \ \ {\ \ a}_{min}^\ast=min\left[a^\ast\left(i\right)\right]$$

$$b_{max}^\ast=max\left[b^\ast\left(i\right)\right],\ \ \ \ \ \ b_{min}^\ast=min\left[b^\ast\left(i\right)\right]$$

Calculate the total color non-uniformity D_Total by the following formula.

$$D_{Total}=\sqrt{\left(L_{max}^\ast-L_{min}^\ast\right)^2+\left(a_{max}^\ast-a_{min}^\ast\right)^2+\left(b_{max}^\ast-b_{min}^\ast\right)^2}$$

Conclusion

Shading describes a decrease in image brightness from the center to the corners or a variation of color over the imaging field that often occurs in cameras with a small sensor. Shading, therefore, influences image quality by creating unwanted dark or shaded edges.

When visualizing the shading of a camera system, it is easiest to capture a flat field image, a photograph of white paper with uniform illumination, or a photograph of a uniform diffuse light source such as the opening of an integrating sphere.

When we test for camera shading in our test lab, we closely follow the methods presented in ISO 17957. We have found that using a matt diffuser chart provides us with the best results for an overall evaluation of shading.