There are phenomena in the area of physics and especially in optics that cannot be explained by geometry. A simple example is a water wave that strikes the entrance of a harbor. If this harbor entrance is narrow the new wave that extends in the harbor has the form of a wave as if a stone was thrown into the water. You can see the wave without being able to see the sea from which the wave came from.
A similar phenomenon can be observed with light. If light is viewed as particles that follow a straight line and reach a sensor behind a diaphragm. But this is not the case. The light also falls onto areas that should not get light if it would follow the particle theory. Therefore even the best lenses show an Airy circle caused by diffraction and this circle gets bigger the smaller the opening of the diaphragm is.
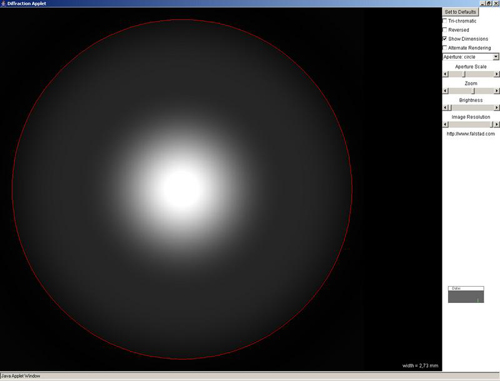
The diffaction image (Airy circle) shows a bright center that is circled by darker rings with the intensity getting smaller tot he ourside.
The radius of the Airy circle being the bright center is calculated from
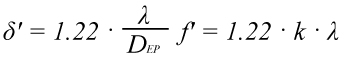
with
δ’ = radius of the Airy circle
λ = wavelength of the light
DEP = diameter of the entrance pupil
k = f-number
The bigger the f-number the bigger the Airy circle. The question that now arises is: when does diffraction become the limiting factor for the reproduction of fine detail meaning resolution. To answer this question we have to look at when can the Airy circles be distinguished by a human being? This was investigated by Lord Rayleigh in 1879. He found that the circles can be distinguished with the human eye when the intensity between the circles decreases to less than 81% of the maximum. This is exactly the case when the distance between the circles equals their radii.
Projected onto a digital camera the radius of an Airy circle should be smaller than the distance between two pixels. To calculate the acceptable size of an Airy circle and from there the largest f-number for which the diffraction does not limit the resolution we have to know the size of the pixels. The simplest way to do determine the pixel size is to divide the sensor width by the amount of pixels.
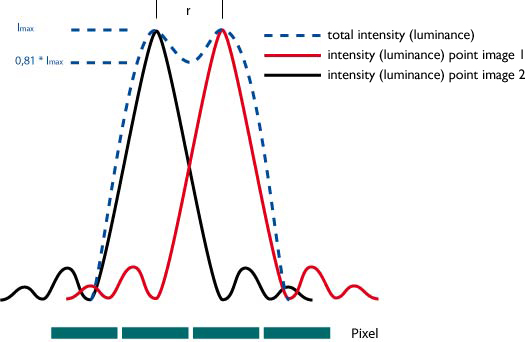
The diffraction structure of two points.
If the distance equals the radius the human eye can distiguish the two circles.
| f-number | diameter of the Airy circle [μm] |
| 1.8 | 1.10 |
| 2 | 1.22 |
| 2.8 | 1.71 |
| 4 | 2.44 |
| 5.6 | 3.42 |
| 8 | 4.88 |
| 11 | 6.71 |
| 16 | 9.76 |
| 22 | 13.42 |
| 32 | 19.52 |
The correlation of the diameter of the Airy circle and the f-number.
| Sensors | Height [mm] |
Width [mm] |
Diagonal [mm] |
Number of pixel (width) |
Pixel size [mm] |
Limiting aperture |
| Canon EOS 1Ds | 24 | 36 | 43.3 | 4992 | 0.0072 | 11.8 |
| Canon EOS 1D | 19.1 | 28.7 | 34.5 | 3504 | 0.0082 | 13.4 |
| Nikon D 70 | 15.6 | 23.7 | 28.4 | 3008 | 0.0079 | 12.9 |
| Fujifilm S3Pro | 15.5 | 23 | 27.7 | 3024 | 0.0076 | 12.5 |
| Canon EOS 200D | 15.1 | 22.7 | 27.3 | 3504 | 0.0065 | 10.6 |
| Sigma SD 10 | 13.8 | 20.7 | 24.9 | 2268 | 0.0091 | 15.0 |
| 4/3" (e.g. Olympus E300) | 13.5 | 18 | 22.5 | 3264 | 0.0055 | 9.0 |
| 2/3" (e.g. Sony DSC-F828) | 6.8 | 9.0 | 11.3 | 3264 | 0.0028 | 4.5 |
| Panasonic LX-1 (1/1.65", 16:9) | 5.0 | 8.9 | 10.3 | 2880 | 0.0031 | 5.1 |
| 1/1.18" (e.g. Konica Minolta DiMAGE X1) | 5.6 | 7.5 | 9.4 | 3264 | 0.0023 | 3.8 |
| 1/1.25" (e.g. Fujifilm FinePix E510) | 4.1 | 5.4 | 6.8 | 2592 | 0.0021 | 3.4 |
| 1/3.2" (e.g. Casio Exilim S100) | 3.2 | 4.2 | 5.3 | 2048 | 0.0021 | 3.4 |
The Table shows the f-number for the diffraction limit of the given cameras.
Larger f-numbers limit the resolution of the camera.
As the table shows the diffraction limit for a digital SLR starts at app. F 11. For consumer cameras the diffraction limit can start at f-stops below 4.
Our example images taken with a Panasonic LX-1 show that even at f 5.6 a decrease in resolution gets visible.

The images show the center of a resolution test chart captured with a Panasonic LX-1 at f-stop 4, 5.6, and 8 (from left to right). It is visible that diffraction causes a resolution limit starting at f 5.6.
Conclusion
With resprect to diffraction a digital camera with large pixels has advantages because f stops down to 11 do not cause a decrease in resolution. Large pixels can usually only be found on large sensors. For consumer cameras with small pixels one has to make sure not to use large f-numbers to prevent the loss of resolution.
dw

