Often times the dynamic range that gets reported by imaging sensor manufacturers is based on the max output signal divided by the noise in the dark areas also called the noise equivalent power. The noise equivalent power describes the signal level where the signal is just as great as the noise – a so-called signal to noise ratio of 1. This basically represents the threshold above which a signal can be detected.
The same is done in the ISO 15739 noise standard. Using gray test charts (or a series of uniform sensor illumination levels) the evaluation detects the luminance level where the camera reaches the maximum digital output signal. This gets divided by the luminance level at which a signal to noise ratio of 1 is reached.
This signal to noise ratio does not have a dimension. Often times the value is given in [dB]
which can be calculated from SNR using the equation: SNR[dB] = 20 log(SNR)
Determine signal to noise level
How is the signal to noise ratio for each signal level calculated?
The image is analyzed at a specific signal level (gray patch, or gray level) and the mean value and the standard deviation are calculated.
Mean value:
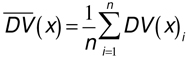
For a digital image x can be photons, luminance, illuminance, irradiance, exposure etc. depending on how the input value is given. On the output side DV is digital output value in the bit depth given by the A/D conversion. i represents the pixels that get averaged. ISO 15739 selects luminance (L) as the input value.
Standard Deviation:
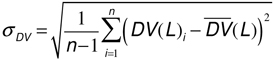
For a linear system L is proportional to DV(L) with a factor K being the gain (or overall system gain, see EMVA 1288) which is constant for each signal level. In this case we can write:
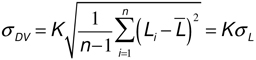
with L being the signal the signal to noise ratio is defined as:
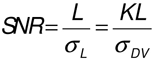
for nonlinear systems K varies with the signal level and needs to be determined for each level. In this case the varying gain is called incremental gain (ISO 15739). This also means that the equation for SNR is only valid in areas where the standard deviation is relatively small and falls within a linear part of the signal.
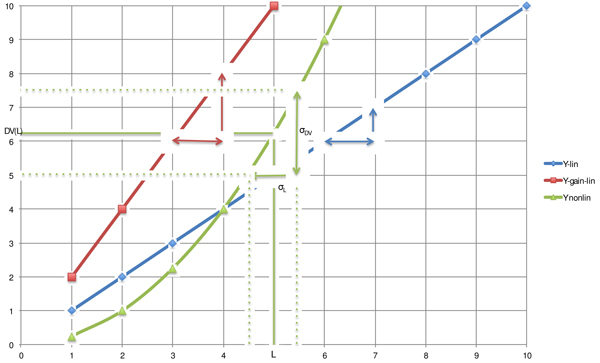
Figure 1: The blue line shows a system that is strictly linear without a gain. The red line represents a linear system with a constant gain (factor) and the green line shows a non-linear system. Within a small area of the green function the gain is also constant and can be used to calculate the signal to noise ratio.
dw

