Introduction
GEOCAL is a camera calibration tool that uses laser technology to project a grid of light spots, enabling precise geometric calibration without traditional test charts. Geometric calibration enhances camera accuracy in industries like automotive and security.
During the product development phase of GEOCAL, we have already involved customers who use other standard geometric calibration methods to develop their products or as a service. These methods are well-established and have been proven to work. In this paper/tech note, we will compare the results of these methods with the results of a geometric calibration performed with the GEOCAL V1.4 software. Version 1.4 is a significant step towards higher flexibility, reliability, and accuracy.
Camera 1
PhaseOne offers geometric calibration of their cameras to customers involved in, e.g., geospatial imaging, requiring a high degree of accuracy in the data they capture. They were kind enough to provide us with a PhaseOne camera together with their results of the current calibration for comparison.
The data below is the camera and the applied hardware and software.
- Camera: PhaseOne iXM-RS150F-RS
- Focal length: 50 mm
- Pixel pitch: 3.76 µm
- Sensor resolution: 14204 px * 10652 px
- GEOCAL used: GEOCAL XL
- GEOCAL Software: V1.4.0
- Applied distortion model: Even_Brown_Model
Even though GEOCAL only requires a single image for geometric calibration, we analyzed three images using GEOCAL software to make sure repeatability is given. The focal length is provided in pixels and converted in mm by applying the pixel pitch. The deviation between the methods is based on the average of the three measurements.
Results
As Phase One states the coefficients of the undistortion function, we cannot directly compare the distortion coefficients calculated by GEOCAL Software. Still, we can compare the acquired focal length and principal point. Here is a comparison of both methods.
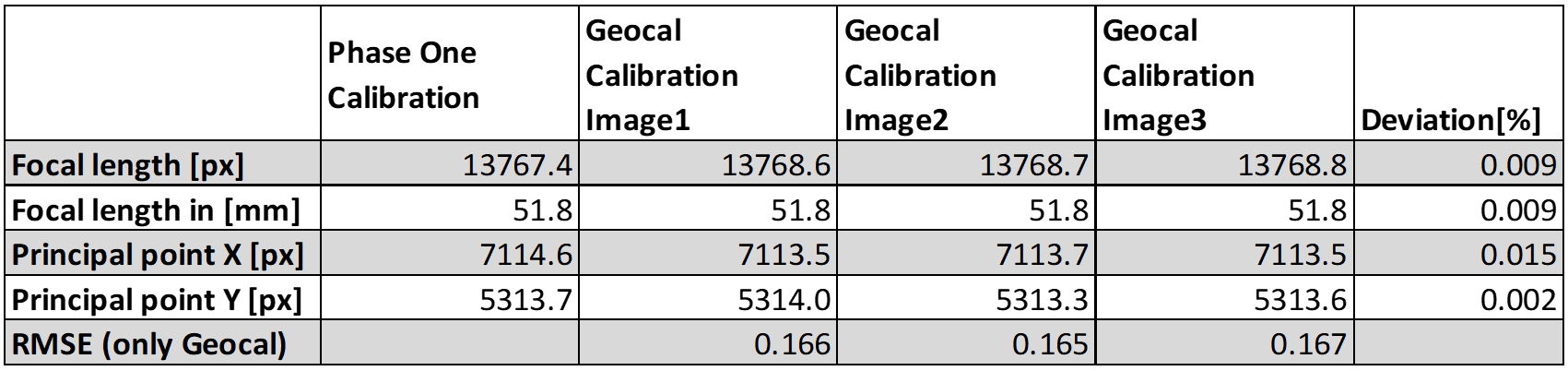
We can see that the difference between both methods regarding focal length and principal point is small. In addition, the Root Mean Square Error (RMSE) value is a fraction of a pixel, which shows that the reprojected grid is very close to the actual detected grid. The RMSE represents the average offset from detected points to the reprojected points in pixels and is the most significant indicator for good geometric characterization.
Camera 2
An automotive customer provided a golden sample camera with known reference data for this comparison.
The data below is the camera and the applied hardware and software.
- Camera: Leopard Imaging
- The angle of view: approx. 120°
- Sensor resolution: 3840 px * 2160 px
- GEOCAL used: GEOCAL XL
- GEOCAL SW: V1.4.0
- Applied distortion model: Custom
- Number of variant coefficients: 4
Results
We took four images, analyzed them with our GEOCAL software, and found that the focal point and focal length also showed little deviation. Again, the deviation between the methods is based on the average of all four GEOCAL measurements.

Having the focal length and the principal point correct, we got everything we need for the intrinsic camera matrix, which is crucial for valid undistortion. The distortion coefficients at that point in the development phase were not yet comparable.
Camera 3 - Checkerboard vs. GEOCAL
We also compared the GEOCAL Calibration with the well-known OpenCV Checkerboard calibration based on our TE251 distortion chart analysis to get a better impression of the performance.
The data below is the camera and the applied hardware and software.
- Camera: Canon Powershot G5 X
- Focal length: 9 mm
- Sensor resolution: 5536px * 3693 px
- GEOCAL used: GEOCAL XL (SN: GC-10004)
- GEOCAL SW: V1.4.1
- Applied distortion model: Even_Brown_Model
- Test chart for validation: TE251
- Analysis Software: iQ-Analyzer-X 1.9
The first step was to take a picture of the GEOCAL XL. To ensure that the dots were clearly visible, we reduced the exposure time as much as possible, set the ISO to its lowest setting, and set the aperture to 11. Then, we ensured that the rotation was as low as possible by keeping the 0th order, the brightest dot, in the image center and the camera horizontally with a spirit level.
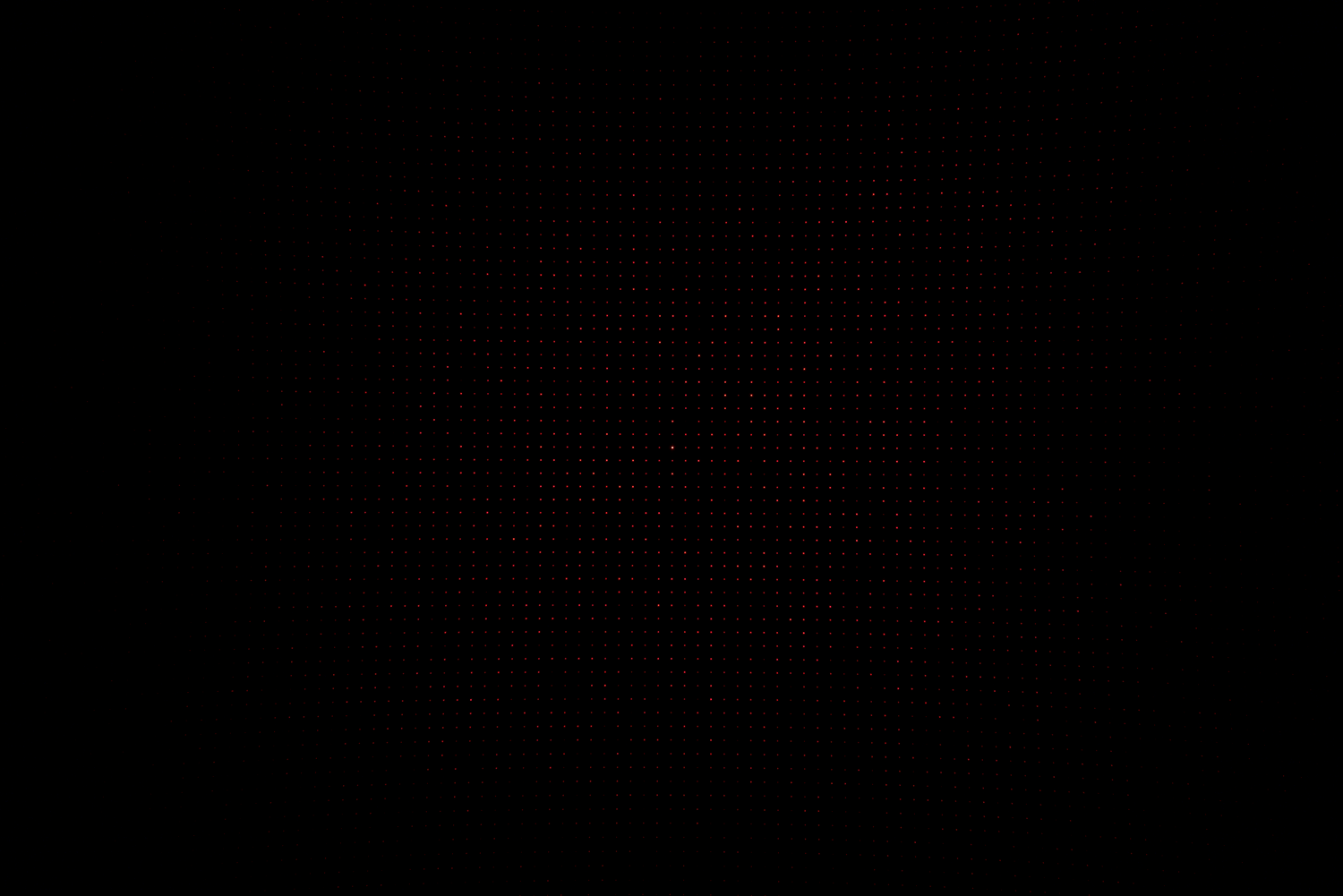
The image seems to be underexposed, but this is a result of the small size of the dots, which is expected. We analyzed it with GEOCAL Software 1.4.1, applying the following configuration.
- Distortion Model: Even_Brown_Model
- Number of radial coefficients: 3
- Number of tangential coefficients: 0 (these are more applicable in the case of a decentered or misaligned lens)
The next step was to perform the OpenCV checkerboard calibration.
To start the checkerboard calibration, we need at least ten images from a squared checkerboard pattern with a defined number of squares. These are the images we used:

We used an example script from the OpenCV documentation for the checkerboard calibration.
OpenCV correctly detected all points. The calibration took around 5 seconds with the GEOCAL software and 95 seconds with the OpenCV code on the same PC.
After both calibrations, the intrinsic parameters and the distortion coefficients looked like this:
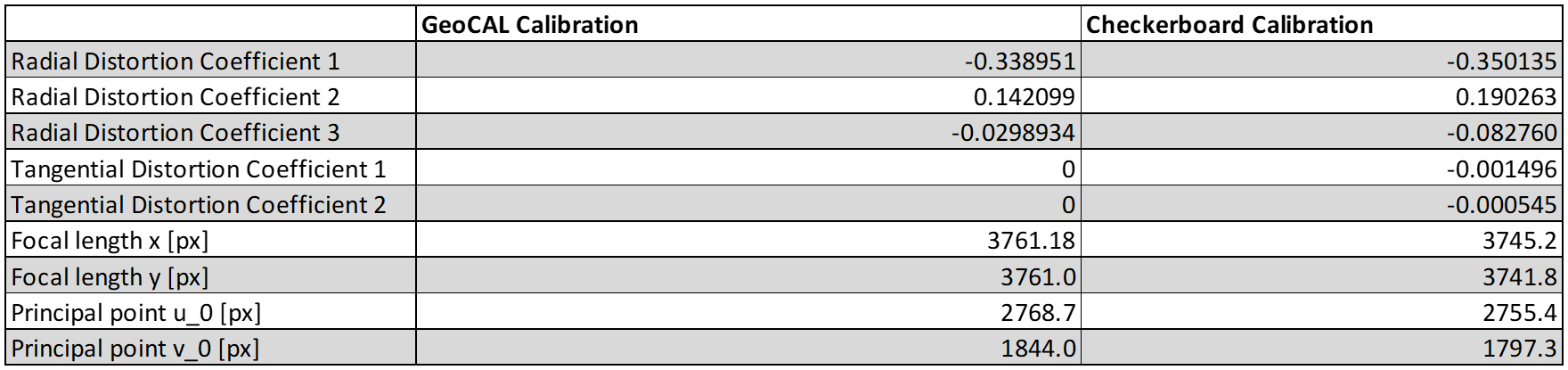
These parameters are all we need to undistort the image of the TE251. We did the undistortion with the GEOCAL and Checkerboard parameters in Python using the OpenCV undistort() function. Here is our input image:
Images after applying undistort().

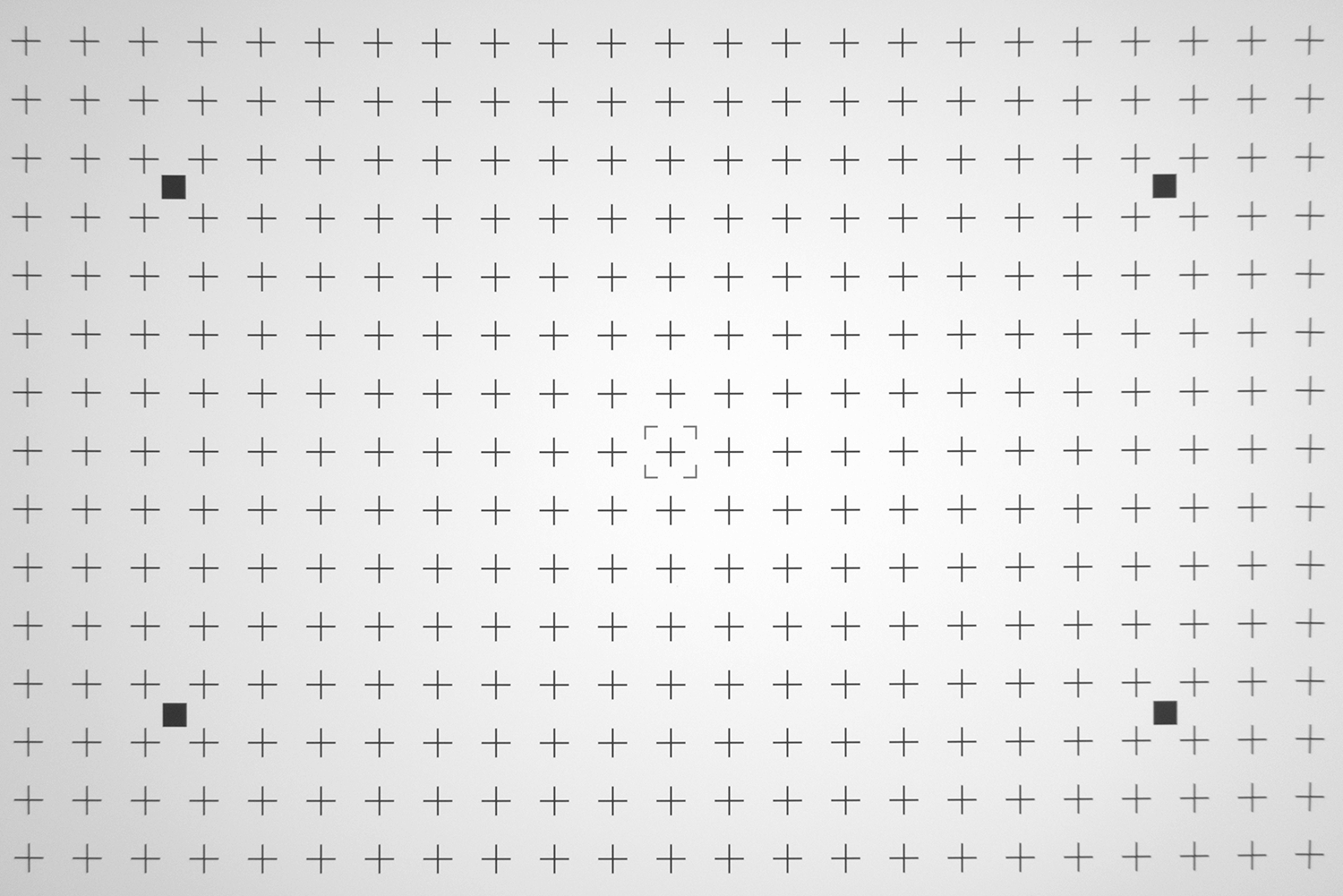
Undistorted image using the checkerboard method (left) and the GEOCAL method (right).
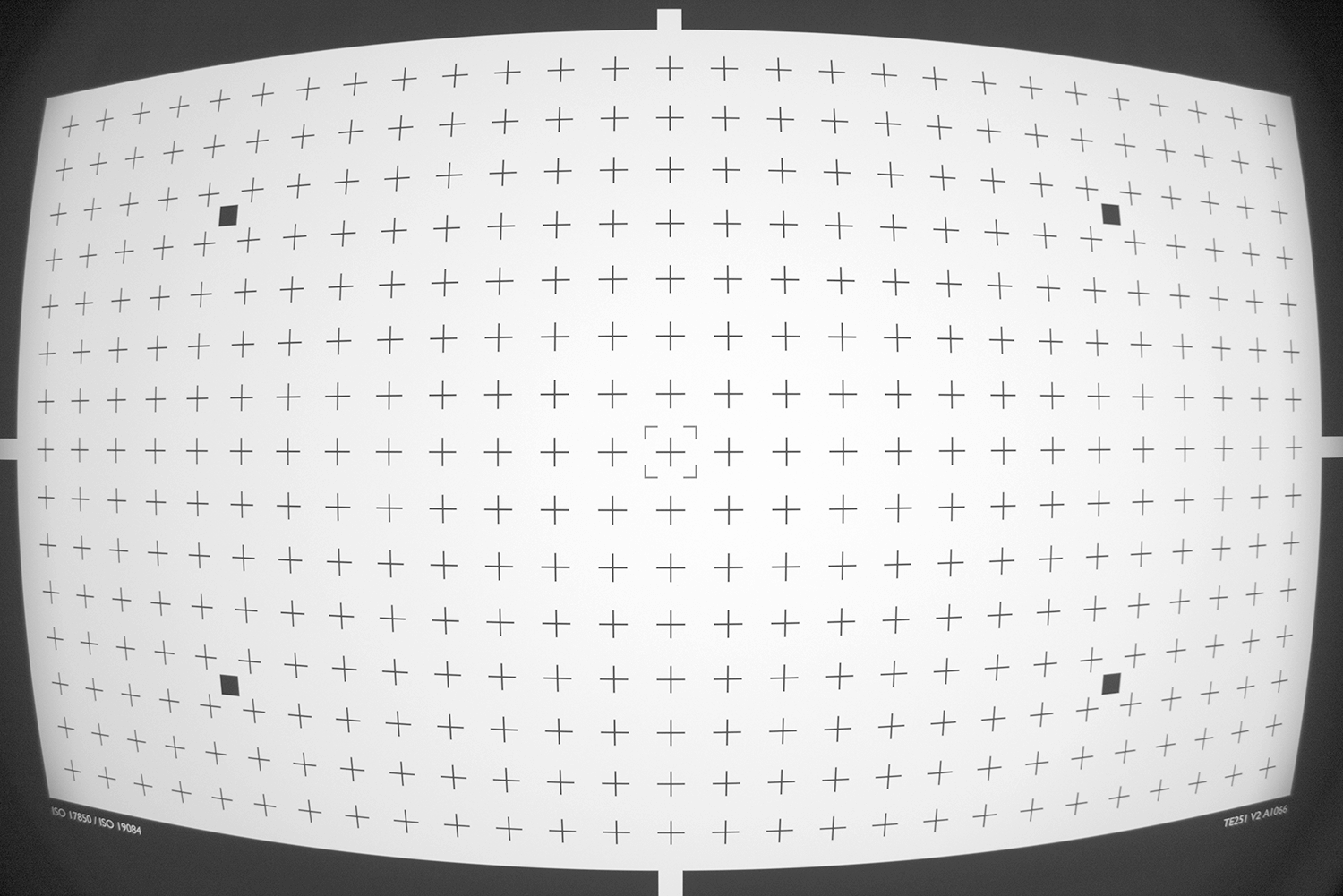
Visually slight differences are noticeable in the corners. We can get a better impression of the performance by measuring the remaining distortion in these undistorted images with iQ-Analyzer-X.
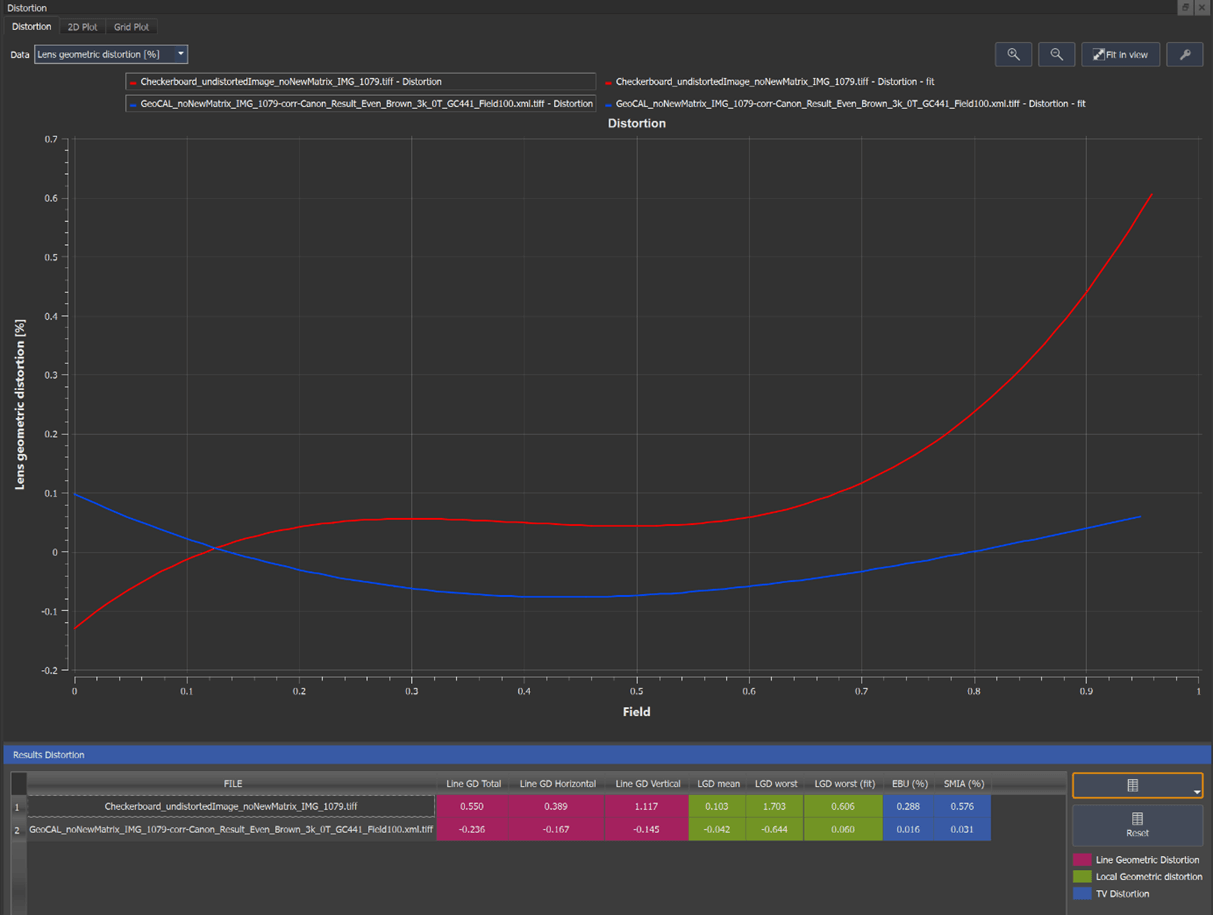
Both methods show Local Geometric Distortion(LGD) close to zero up to 70% of the field; above 70%, the GEOCAL performs better. The lines in the plot above represent the average LGD for a specific radius/field. Imagine it is the LGD of all detected crosses in the TE251 with the same radius. To learn more about the calculation of LGD, which is a part of ISO17850, visit our website library - distortion.
The 2D plot provides a good overview of the distortion distribution over the entire image field. However, the alignment between the camera and the chart is a huge factor in the appearance of both plots.
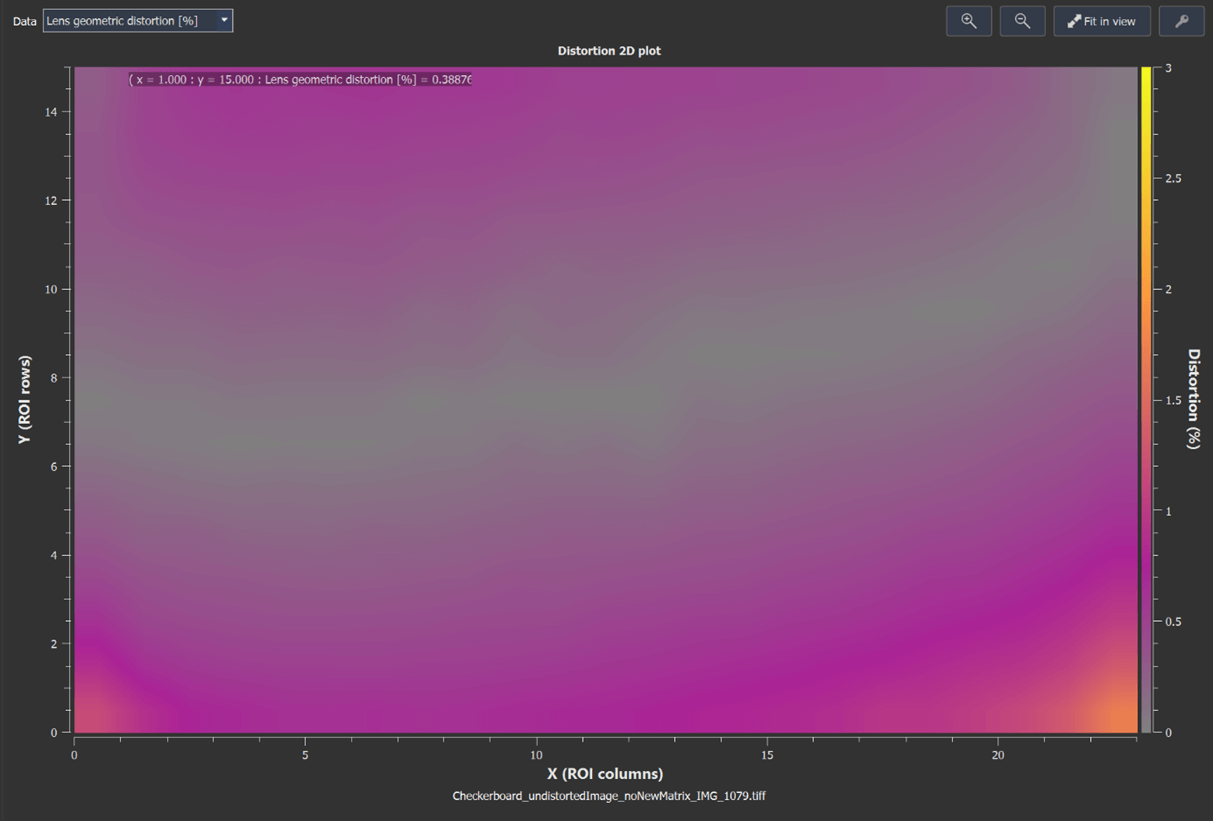
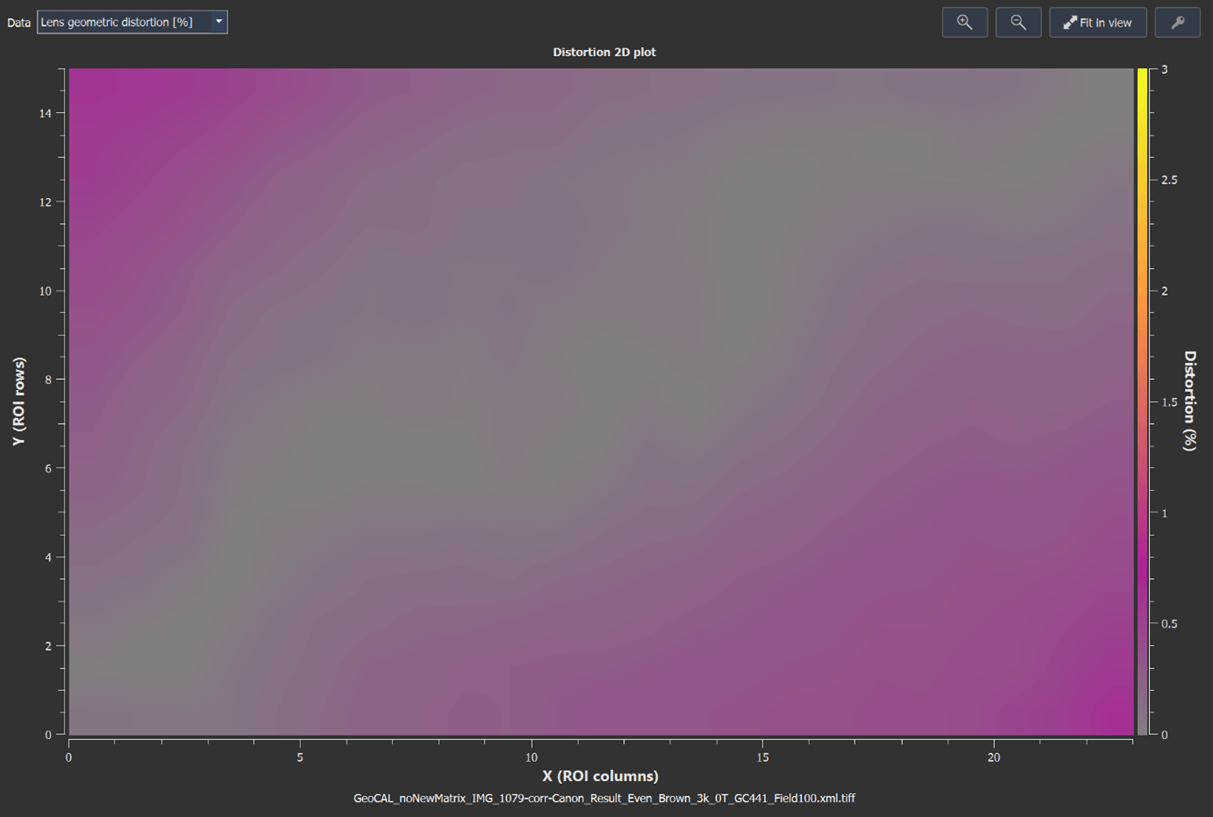
Test results of the checkerboard methods (left) and the GEOCAL method (right).
Please note that we did not use the tangential coefficients in the GEOCAL calibration, while the Checkerboard calibration does apply them. We noticed that leaving out the tangential coefficients in this case leads to better results, visually and objectively.
Summary
In the first two examples, the GEOCAL calibration proved to be quite accurate in finding the focal length and principal point, which are the crucial parameters of the intrinsic camera matrix. The Checkerboard vs. GEOCAL comparison shows similar results to the OpenCV Checkerboard calibration when using OpenCV's undistortion algorithm. It performs better in terms of ease of use because it does not require as many images to be captured. One properly exposed and aligned image is enough. Also, it requires much less space for its setup. However, to use the GEOCAL calibration, the camera must be able to focus on infinity or at least close to infinity to provide sharp points. It should also be possible to adjust the exposure to avoid saturation of the points. The time required for calibration was much less with GEOCAL, making it very interesting for applications requiring speed, high throughput, and precision.
Contact us
Contact us at for more information on GEOCAL
Download the PDF of this article from our library.

